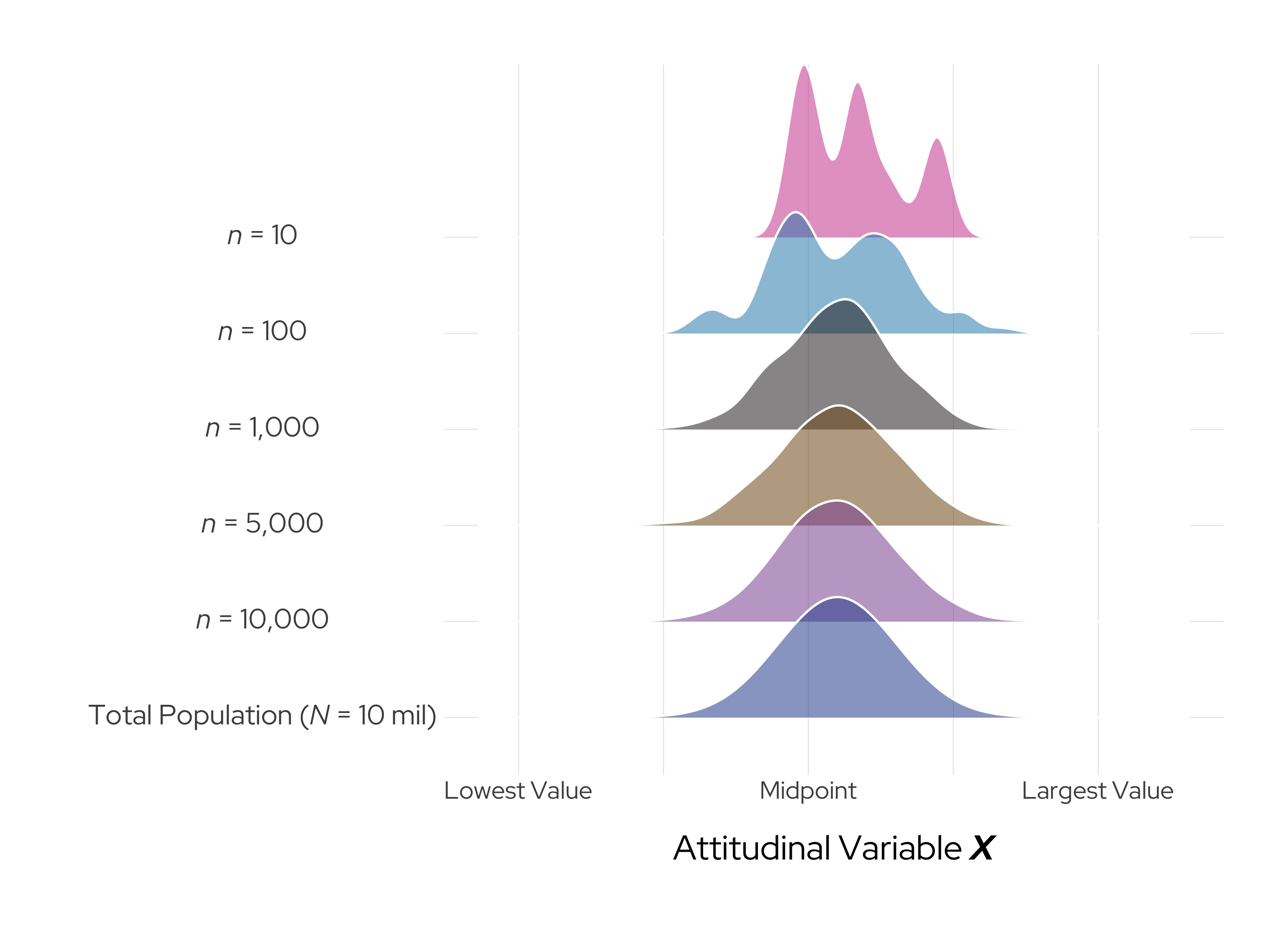
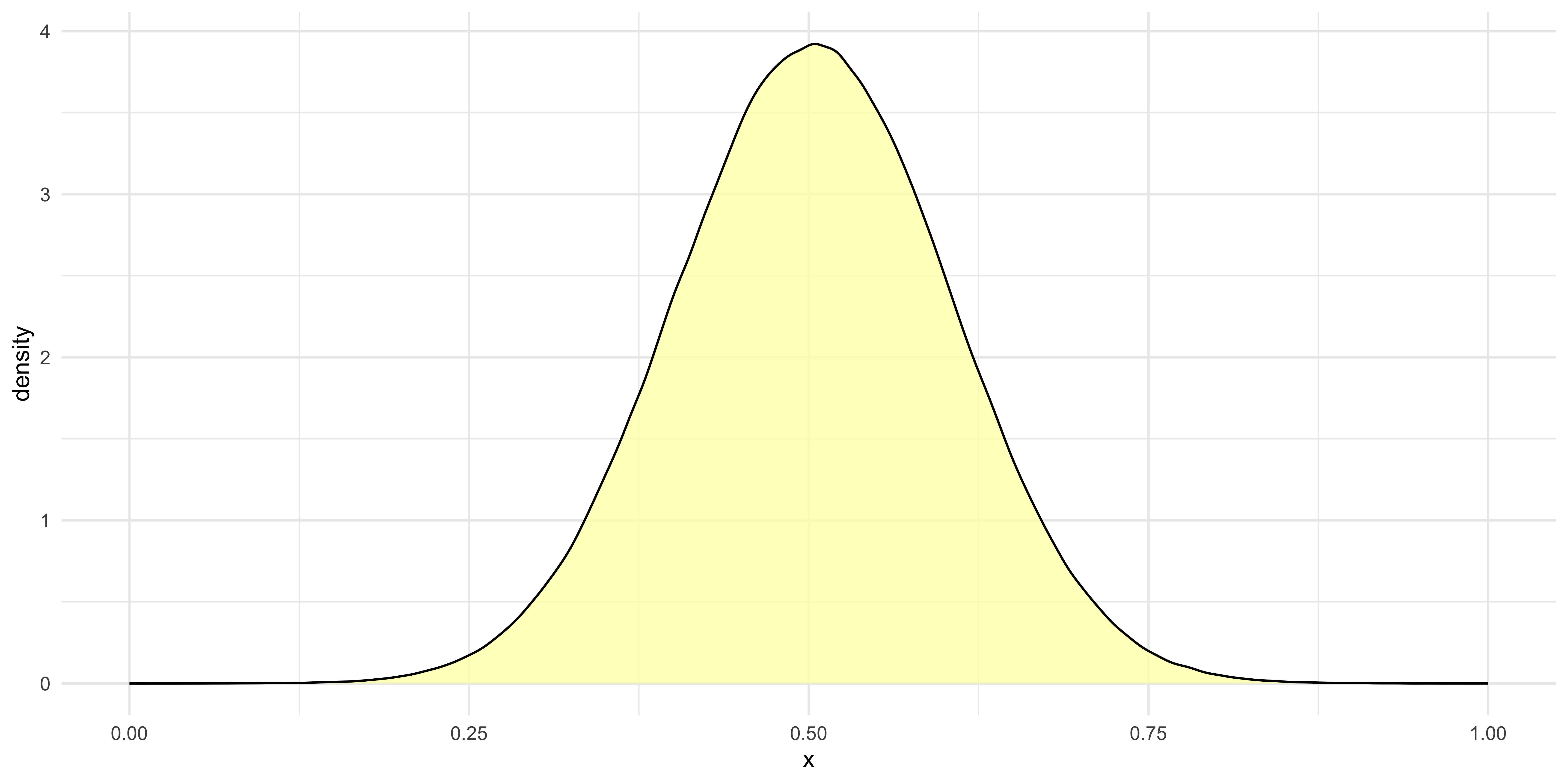
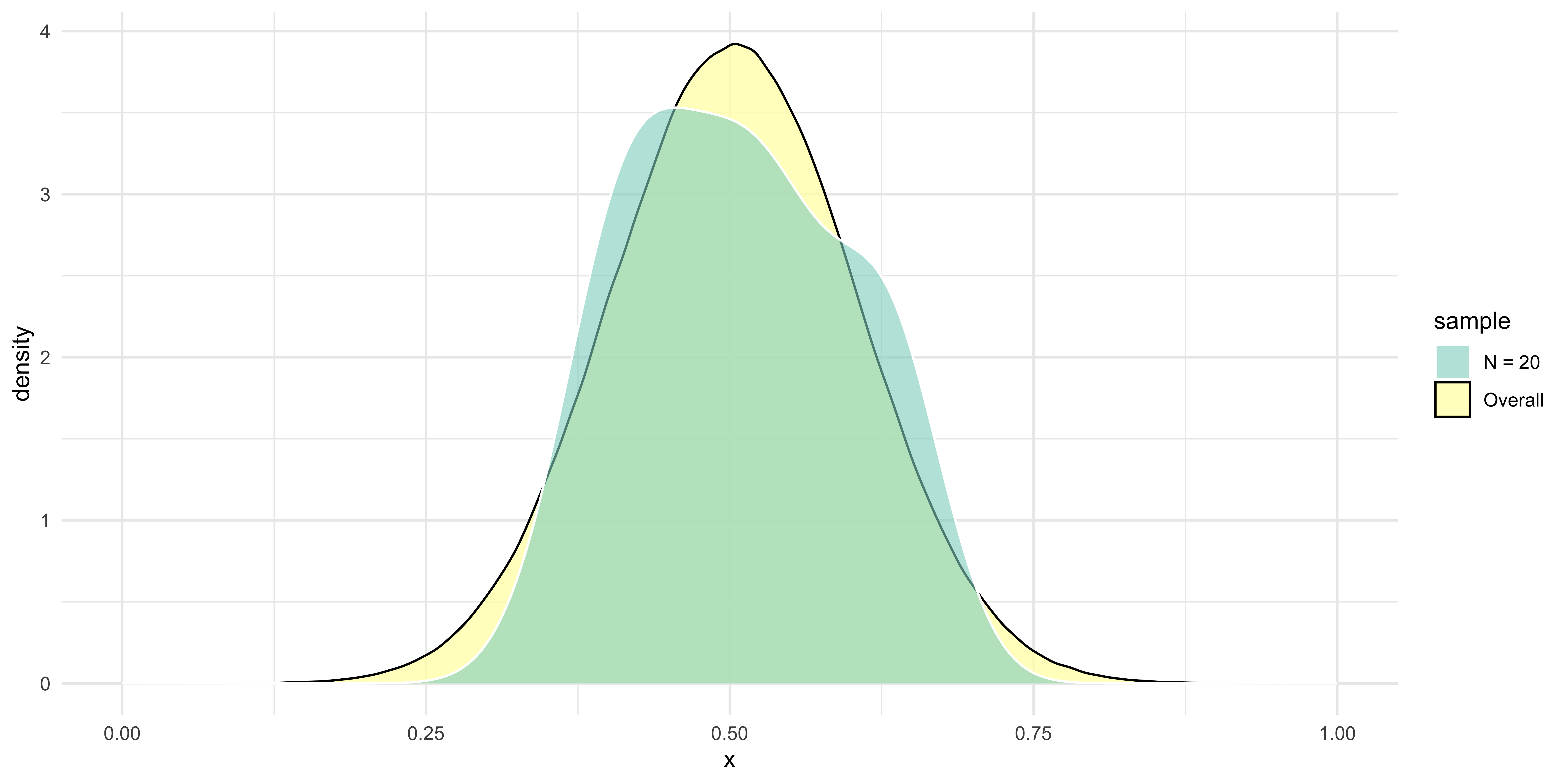
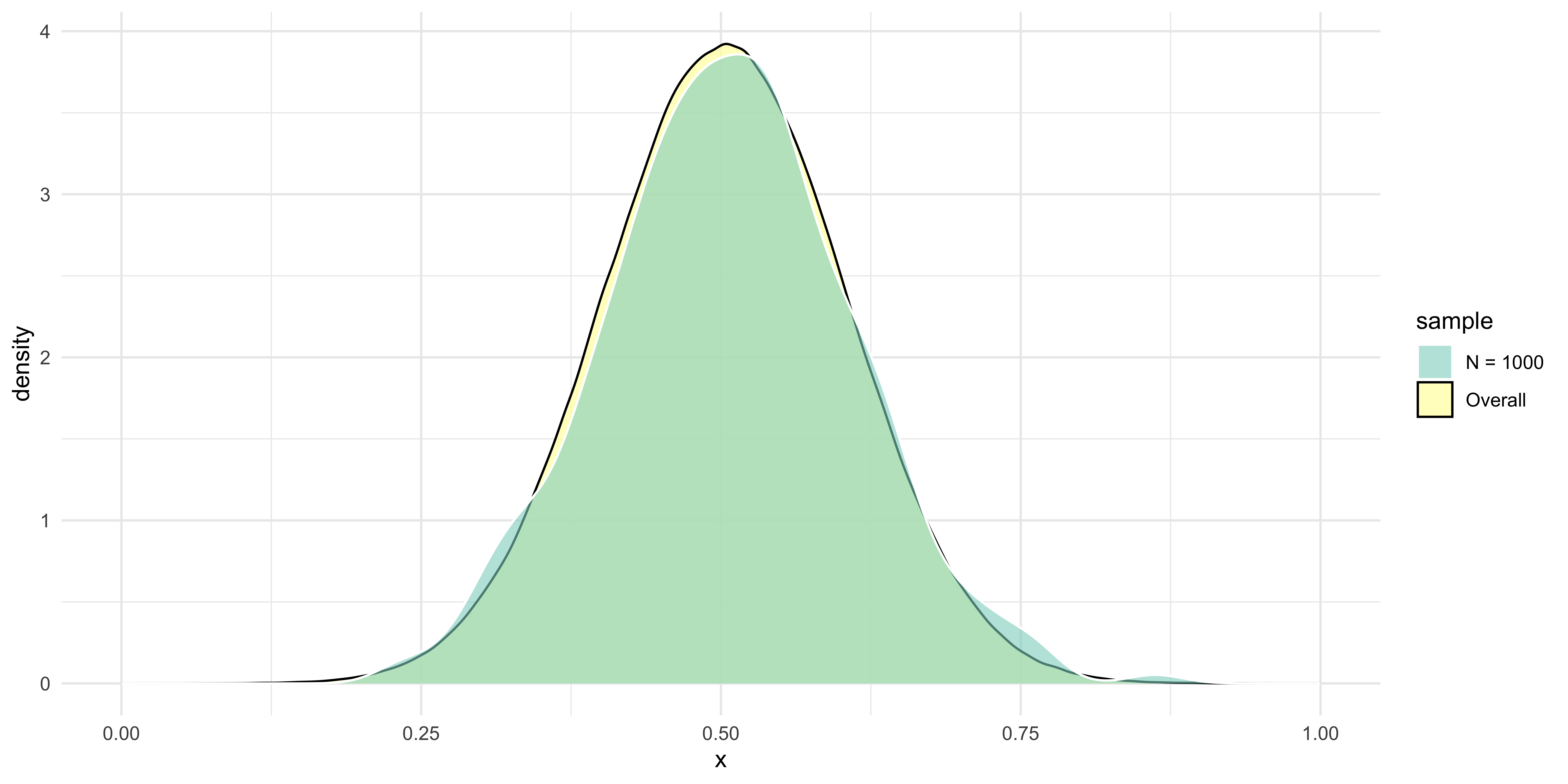
Show the underlying code
library(tidyverse)
# Generating a population with one million people
set.seed(101)
population <- tibble(x = rnorm(1e6, mean = 0, sd = 27),
sample = "Overall") |>
mutate(x = scales::rescale(x, to = c(0, 1)))
ggplot(population,
mapping = aes(x = x)) +
geom_density(alpha = 0.75, fill = "#FFFFB3") +
theme_minimal()